数式的な解説
ARマーカーの持つ値
各ARマーカーから得られる値は以下の3つ
-
座標の値:$[tx, ty, tz]$
-
回転の値:$[rx, ry, rz]$
-
ID :$id$
認識できたARマーカーを$AR = [AR_0, \ldots , AR_n]$として、各ARマーカーの持つ値を$AR_i.id$のように表す。
追従対象の情報を計算
追従対象の情報を得る式を説明する。図の灰色の部分は自動追従で使わない情報。
-
座標
追従対象の座標$[tx,ty,tz]$は
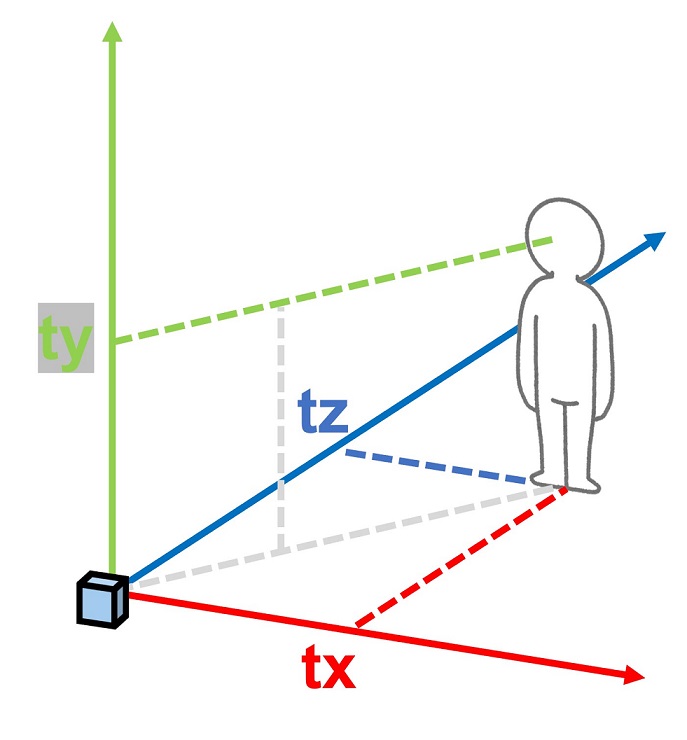
$[tx, ty, tz] = [\frac{\sum_{n}^{i=0}AR_i.tx}{n}, \frac{\sum_{n}^{i=0}AR_i.ty}{n}, \frac{\sum_{n}^{i=0}AR_i.tz}{n}]$
で求める。 -
回転
追従対象の回転$[rx,ry,rz]$は
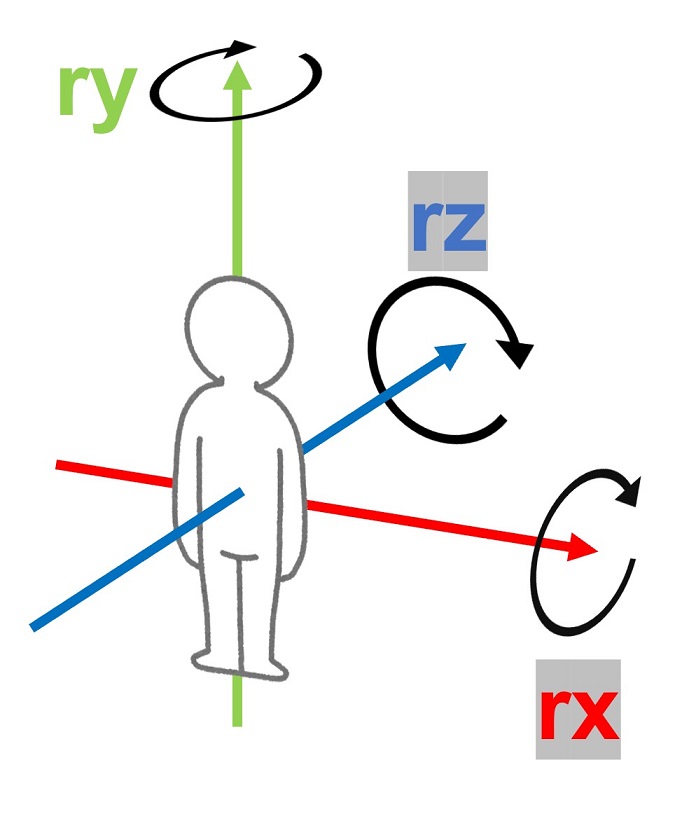$[rx, ry, rz] = [\frac{\sum_{n}^{i=0}AR_i.rx + AR_i.id \times 90}{n},
\frac{\sum_{n}^{i=0}AR_i.ry + AR_i.id \times 90}{n},
\frac{\sum_{n}^{i=0}AR_i.rz + AR_i.id \times 90}{n}]$
で求める。
ただし、$AR_i.id$が$0$で、回転の値が負の場合$+360$する。 -
方向
追従対象の方向はそれぞれ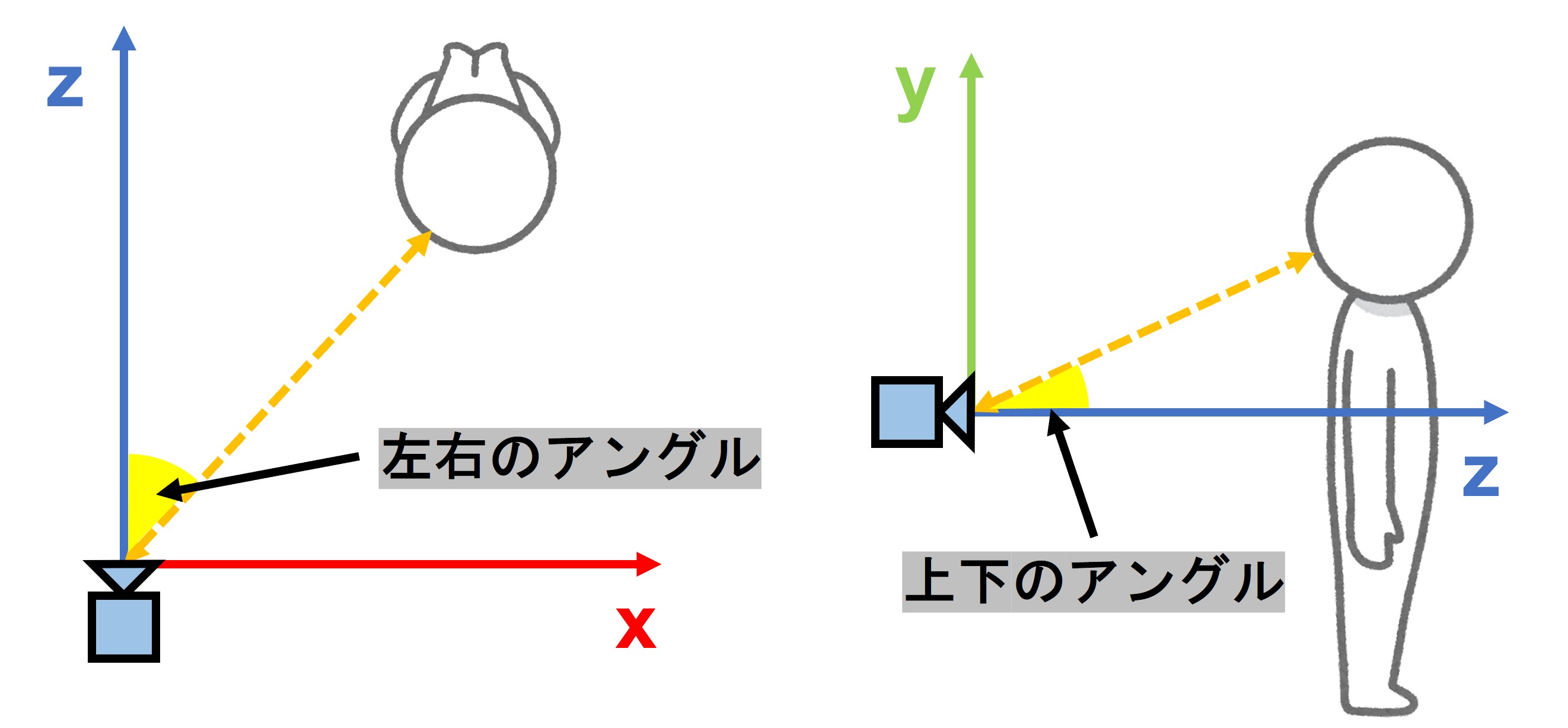
- 左右の方向 : $arctan(\frac{tx}{tz})$
- 上下の方向 : $arctan(\frac{ty}{tz})$
で求める。
-
距離
カメラから追従対象の距離は
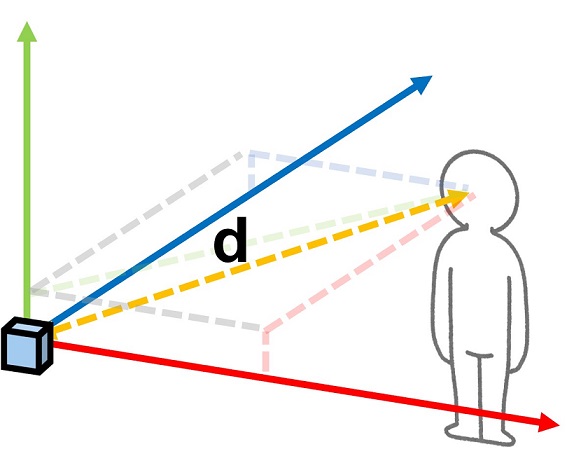$d = \sqrt{tx^2 + ty^2 + tz^2}$
で求める。
コード
private void CalcTargetRotation(ARMarker[] markers)
{
if (markers.Length < 1) return;
Array.Clear(position, 0, position.Length);
Array.Clear(rotation, 0, rotation.Length);
int i, j;
for (i = 0; i < markers.Length; i++)
{
for (j = 0; j < markers[i].rArr.Length; j++)
{
if (markers[i].ID == 0 && markers[i].rArr[j] < 0) markers[i].rArr[j] += 360;
rotation[j] += markers[i].ID * 90 + markers[i].rArr[j];
}
for (j = 0; j < markers[i].tArr.Length; j++)
{
position[j] += markers[i].tArr[j];
}
}
for (j = 0; j < position.Length; j++) position[j] /= markers.Length;
for (j = 0; j < rotation.Length; j++) rotation[j] /= markers.Length;
if (position[2] == 0) return;
angle[0] = Math.Atan2(position[0], position[2]) * (180 / Math.PI);
angle[1] = Math.Atan2(position[1], position[2]) * (180 / Math.PI);
distance = Math.Sqrt(Math.Pow(position[0], 2) + Math.Pow(position[1], 2) + Math.Pow(position[2], 2));
}